Résultat de l’effet Doppler/Fizeau dans l’air. Et application à la relativité restreinte d’Einstein .

1)Introduction
L’effet Doppler dans l’air est assez connu, au bord d’une route, par exemple, si un véhicule Klaxonne et vient vers nous,
on entend distinctement un son très aigu , qui devient grave quand il s’éloigne. Pour les courses de formule 1 c’est
caractéristique, quand la voiture passe devant le micro et s’éloigne ensuite.

2) Calcul emetteur fixe , récepteur en mouvement (Le récepteur reste dans l' axe du mouvement , pas d 'effet Doppler latéral )

.Le travail est plus simple si l’on considère des balles tirées à intervalles réguliers, au lieu d’ondes, c’est la même chose, on utilise alors des particules. Au repos on a : c=Lx f où f est la fréquence des tirs, (10balles par seconde par exemple) c une constante, la vitesse des balles dans l’air, et L la longueur d’onde, la distance entre 2 balles consécutives .Exemple, la vitesse est de 100m/s, la fréquence 10/s, la longueur d’onde sera de 10 m. L’inverse de la fréquence, c’est la période p=1/f .Exemple ici la période, est de 1/10 s, c’est le temps entre 2 balles consécutives.
Le récepteur avance en direction des balles à vitesse v , balles qui avancent aussi à vitesse c.
.On va calculer le temps t1 qu’il faudra à ce système pour rencontrer 2 balles consécutives. La distance parcourue par la voiture pendant ce temps t1 est d=v.t1 , la balle parcourt d’=ct1 avec d+d’=L... L Longueur d'onde émise, hé oui la distance entre 2 balles. Donc t1(c+v)= L=c/f .Comme t1 , est la période apparente que reçoit le récepteur en mouvement t1=1/F‘;.. F‘ fréquence apparente . On sort alors F'=f.(v+c)/c quand v tend vers (est égal à) c f’ tend vers 2 f. De même , si le récepteur fuit l’émetteur v passe en –v, et la fréquence s’annule pour v=c , puis la fréquence devient négative , à un moment le récepteur rattrapera le premier train d’onde et ne captera plus rien…

3)Emetteur en mouvement , récepteur immobile

La voiture qui avance vers le récepteur à vitesse v émet ses balles à intervalle régulier, mais une fois une balle émise, elle rattrape un peu cette balle, et émet l’autre balle p secondes plus tard. L’observateur immobile, verra alors arriver sur lui des balles à vitesse c et de longueur d’onde l’=(c-v).p ou (c-v)/f .
Il pourra poser c=l’.f’ avec f’ fréquence apparente du récepteur ; et de suite F''=f.c/(c-v) qui est très différente de la précédente équation .Quand v augmente ; f’ augmente, le son devient plus aigu, on entend ça au bord des routes. On voit que quand v tend vers c , f’ tend vers l’infini, c’est ce qu’on appelle pour un avion le mur du son ! Quand v dépasse c, on dirait que les ondes sont perçues à l’envers ; une sorte d’inversion du temps dans le train d’onde .Pour v=2c, on a f=-f’ , l’avion arrive avant les ondes et ensuite on entend le son inversé …
A noter que si l’émetteur fuit le récepteur la formule devient F''=f.c/(c+v) .Quand la voiture s’éloigne la fréquence est plus petite, le son est plus grave ! Le fameux iiiiiiiioooooooouuuuuuaaaaaaaa !

4)Développement

Avec sa relativité ,Einstein postule, que pour le même phénomène reporté à la lumière, et à
notre univers , on ne devrait pas faire de différence entre ces 2 points de vue (émetteur fixe,
ou émetteur en mouvement ).Pas de repère privilégié dit -il !

On se reporte au problème d'une étoile qui nous émet des flashs, et nous filons vers elle en 1) ;
en 2 on suppose que c'est elle qui file vers nous.:
Dans la 1 façon de voir ;
on a 1) F'=f.((v+c)/c)....... f’ fréquence reçue du récepteur en mouvement .
De même pour la 2ème façon de calculer ;le récepteur file vers l’émetteur.
2) F’’=f.c/(c-v) ......f’’ fréquence reçue du récepteur immobile.
Ce que l'on veut avoir c'est F"=F' , avec les même termes, on va chercher un multiplicateur $
qui corrige la fréquence à l'intérieur du vaisseau ou de l'objet qui file (ou qui semble filer)
Pour 1 on a alors puisque c’est F’ qui bouge F’$=. f.((v+c)/c)
Pour 2 puisque c’est f qui bouge : f’’=f.$.c/(c-v)
On écrit F’=F’’..... f.((v+c)/c)/$ = f.c/(c-v).$ -----f est le même bien sûr, fréquence au repos.

Et bingo $²=(c²-v²)/c² .= 1 - v²/c² $=rac(1-v²/c²) Equation connue en relativité.
On voit ici avec cette correction que la fréquence d’un objet en mouvement est multipliée par
ce coefficient , la fréquence f’’ et f’ reste identique en terme .On peut estimer que ce correcteur
$ ralentit alors le temps dans l’objet en mouvement avec le rapport T’/T=$ T temps au repos.
T’/T=rac (1-c²/v²)
La fréquence relativiste apparente d’un objet lumineux en mouvement est donc F’=f. c/(c-v)$

Après simplifications F’= f .RAC[ (c+v)/(c-v) ]=f.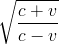
On vérifie que la seconde expression donne le même remarquable résultat !

Une observation assez intéressante de l'effet Doppler a été faite par Roëmer , un astronome du 17 `me siècle.Il a observé les satelites de Jupiter et Io qui voyait un retard dans son occultation suivant la position de la Terre par rapport à Jupiter .Il comprit que c'était à cause de la distance qui séparait les 2 astres : la lumière mettant plus longtemps à arriver quand on est loin, on voit Io tel qu'il était il y a disons 20 mn ; quand la Terre s'approche, on le voit disons tel qu'il était il y a 10 mn;, ainsi , l'air de rien on a gagné 10 mn et Io est 10 mn en avance .Le rapport avec Doppler c'est que lorsque la Terre avance sur Jupiter, on voit sa période de rotation diminuer , je crois que c'est aux alentours des 5 s au lieu de 1,769 jours c'est 1,769 jours et 5 s .Ces 5 secondes s'accumulent pour arriver à près de 10 mn .Quand on s'éloigne de Jupiter , la période de Io augmente... Avec un télescope , si l' on pouvait voir des extraterrestres en s' approchant d' eux , on les verrait en accéléré , et inversement ooooon les verrrrait au raaaaleeentii en s' éloignant !

Grenier Roland 2009 .